The Narrow Gate and Hyperbolic Geometry

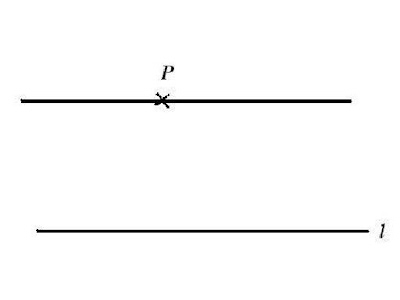
Playfair's axiom: Given a line l and a point P not on that line, there is a unique line that passes through P that does not meet l.

Those of you of a certain age may well have been taught Euclid's five axioms of geometry. You may even be aware of the controversy of the fifth axiom, the famous "Parallel Postulate" which John Playfair expressed (in my eyes) more succinctly and elegantly than Euclid originally did.



The first four axioms were certainly reasonable enough. They remarked on things we might find quite obvious about our reality, e.g. given two points in space, there is a unique line that joins them, or that one right-angle is the same size as another right-angle. The fifth seems less so: why should it be obvious in our reality that there is only one line through P that is parallel to l?


If one considers a straight line to be the path which joins two points with the shortest distance, then the straight lines on the Earth's surface are arcs of circles with the same centre as the Planet. These are different from Euclid's straight lines, but we don't notice the difference when we are crossing the road as the crow flies to get to Tesco's. In the small scales in which we inhabit, these vast arcs of circles (Great Circles as we mathematicians- failed or otherwise- call them) appear to be no different from what Euclid described as a straight line.


The trouble is, on the Earth's surface, Playfair's (and thus Euclid's) axiom is blatantly false.

In the geometry of the Earth, the Parallel postulate is false. There are no such things as parallel lines on the Earth. Admittedly, the geometry of the Earth also breaks others of Euclid's axioms, in fact any geometry in which there are no parallel will break at least one other of the axioms.

That's not the only way that Playfair's axiom could fail: there could be more than one line through P that doesn't meet L. Here Bolyai and Lobachevsky showed that there are geometries which meet all of Euclid's axioms but not the fifth. (If the lines appear curved, that's because you're looking at them with the wrong eyes.)The most useful of these is the hyperbolic geometry which has a constant curvature, like the sphere or the plane. It's a bit tricky to describe; I suppose that the easiest way to describe it is that everywhere you look, it looks like the surface of a saddle. We usually try to flatten it out, but the lines will then look like arcs of circles which meet a boundary circle at right-angles. The boundary circle isn't really there - it's the hyperbolic version of an horizon. It's called the Poincaré disc.

So why am I going through all this mathematics? What's my point?

It's this business of "One True Church" again, the attitude of "this is the only way to God - the Way." It is clear that the way is narrow, the Lord tells us this much. Yet, I invite you to look carefully at the Poincaré disc. All those lines are straight in the reality of this disc and yet there are groups of lines (mathematically called a pencil of lines) which meet at the horizon. However, hyperbolic lines meet more truly at the horizon than lines in Euclidean space; by that I mean, the distance between those parallel lines, which are straight in this geometry, decreases the nearer they get to a common point on the horizon.

I am still trying to fathom in what way Church Unity can be achieved. If the Christian reality is hyperbolic like the Poincaré disc, then maybe we have got to make sure that if we cannot walk together as Christians, then at least we are travelling in parallel directions on an ever narrowing course to the One True Christ Who lies on the horizon of our vision. If our constant intellectualising (mea culpa) seeks to keep us apart, then let us at least have the charity to allow other Christians the opportunity to travel parallel to us in the hope that together we reach the promised land of the Love of Christ.